算法 | Owen

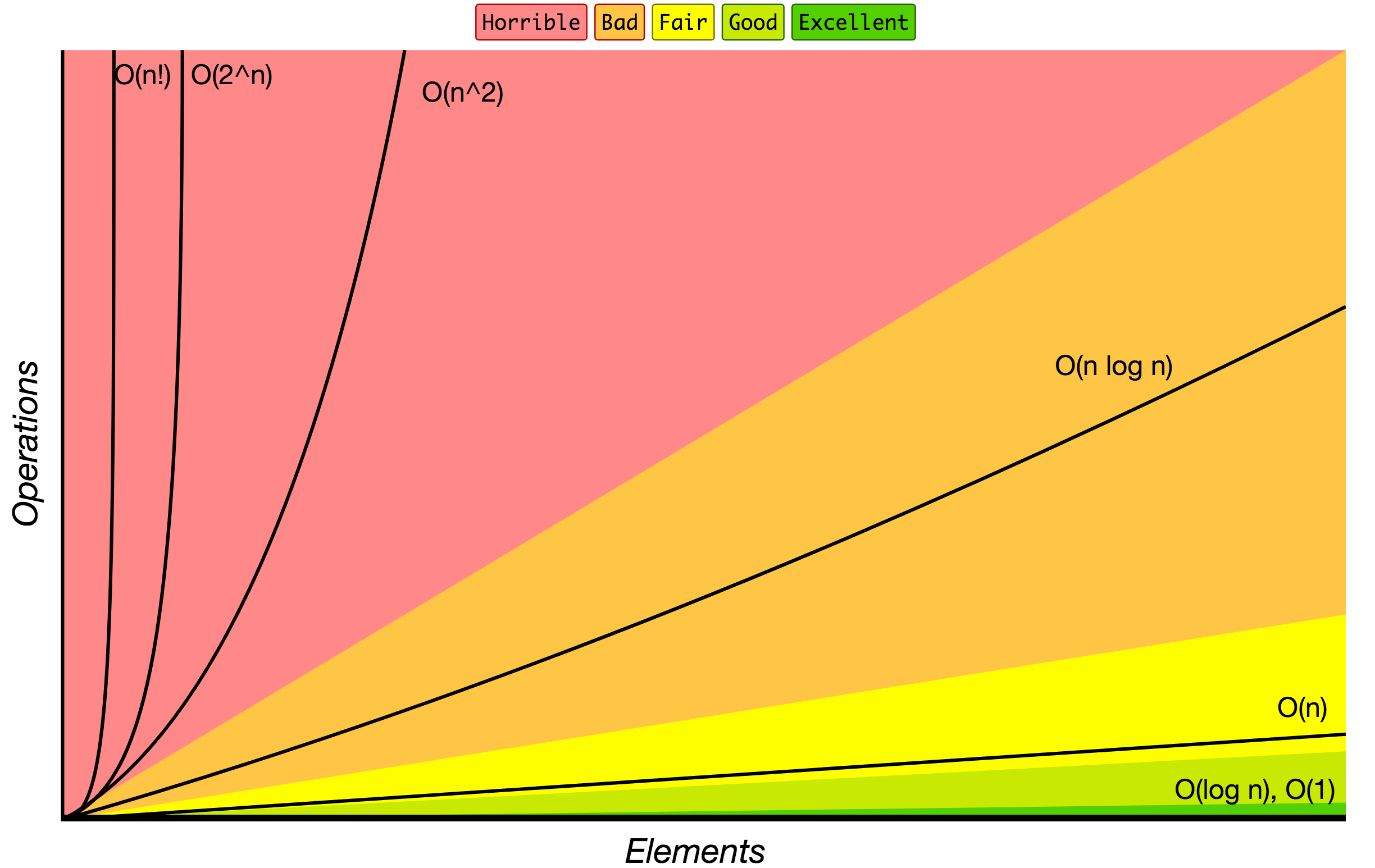
术语

时间复杂度: 一个算法执行所耗费的时间。

一个算法花费的时间与算法中语句的执行次数成正比例,一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。
n称为问题的规模，当n不断变化时，时间频度T(n)也会不断变化，要知道变化时呈现什么规律就引入了时间复杂度概念
算法中基本操作重复执行的次数是问题规模n的某个函数，用T(n)表示，若有某个辅助函数f(n),使得当n趋近于无穷大时，T（n)/f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=Ｏ(f(n)),称Ｏ(f(n)) 为算法的渐进时间复杂度，简称时间复杂度。
空间复杂度: 运行完一个程序所需内存的大小。

一个算法所需的存储空间用f(n)表示。S(n)=O(f(n))　　其中n为问题的规模，S(n)表示空间复杂度。
内排序：所有排序操作都在内存中完成；外排序：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行；
稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面；不稳定：如果a原本在b的前面，而a=b，排序之后a可能会出现在b的后面；

两数之和

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那两个整数，并返回他们的数组下标。你可以假设每种输入只会对应一个答案。但是，你不能重复利用这个数组中同样的元素(自己不能跟自己加起来等于target)。

给定 nums = [2, 7, 11, 15], target = 9

因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]

解答：


/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number[]}
 */
// 方法一  嵌套循环  时间复杂度：O(n^2) 空间：O(2)
var twoSum = function(nums, target) {
    for (let [i,k] of nums.entries()){
         for (let j = i+1; j< nums.length; j++) {
              if(  (target - k) === nums[j]) {
               return  [i,j];
            }
         }
    }
};
// 方法二 嵌套循环 比 方法一 更快
var twoSum = function(nums, target) {
            let len = nums.length;
            for (let i = 0; i<len; i++){
                for (let j = i+1; j<len; j++) {
                   if( (target - nums[i]) === nums[j]) {
                   return  [i,j];
                 }
                }
            }
};
// 方法三 has表   时间复杂度：O(n) 空间：O(n)
/**
 * 存储对应的值 和 索引
 */
var twoSum = function(nums, target) {userManage
      const m = new Map();
      const len = nums.length；
    for (let i = 0; i < len; i++ ) {

        if(m.has(nums[i]) && m.get(nums[i]) !== i){
            return [m.get(nums[i]),i]
        }
            m.set((target - nums[i]),i);
    }

};

//or
var twoSum = function(nums, target) {
      const m = new Map();
      const len = nums.length；
    for (let i = 0; i < len; i++ ) {
        let  res = target - nums[i];
        if(m.has(res) && m.get(res) !== i){
            return [m.get(res),i]
        }
            m.set(nums[i],i);
      }
};

整数反转

给出一个 32 位的有符号整数，你需要将这个整数中每位上的数字进行反转。

假设我们的环境只能存储得下 32 位的有符号整数，则其数值范围为 [−231, 231 − 1]。请根据这个假设，如果反转后整数溢出那么就返回 0。

/**
 * @param {number} x
 * @return {number}
 */
var reverse = function(x) {
     let res =( x+'' ).split("");

    if(res[0] !== '-'){
        let num = parseInt(res.reverse().join(''),10);
         if( num> Math.pow(2,31) -1){
             return 0
         }
       return num;
    }else{
        res.reverse().pop();
      let num = parseInt(res.join(''),10);
        if( num> Math.pow(2,31) -1){
             return 0
         }
        return  '-' + num;
    }
};

回文数

判断一个整数是否是回文数。回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。

输入: 121 输出: true
输入: -121 输出: false 解释: 从左向右读, 为 -121 。从右向左读, 为 121- 。因此它不是一个回文数。
输入: 10 输出: false 解释: 从右向左读, 为 01 。因此它不是一个回文数。
注意 0 是回文数

进阶: 不将整数转为字符串来解决这个问题

/**
 * @param {number} x
 * @return {boolean}
 */
 // 方法 一 转化未字符串
var isPalindrome = function(x) {

    return  x < 0? false: (parseInt((x+'').split('').reverse().join('')) === x ? true : false);
};
/**
 * 方法二  中间数的右边反转后 等于 左边
 * 提取中间数的右边 通过 *10 、 %10 来提取
 * */
var isPalindrome = function(int) {
   if(int < 0 ||  (int%10 === 0 && int !== 0)) return false;

    let num = 0;
    while (int > num ){
        num = num * 10 + int % 10;
        int = parseInt(int/10);
    }
console.log(int,num)
    return  int === num || int === parseInt(num/10);
};